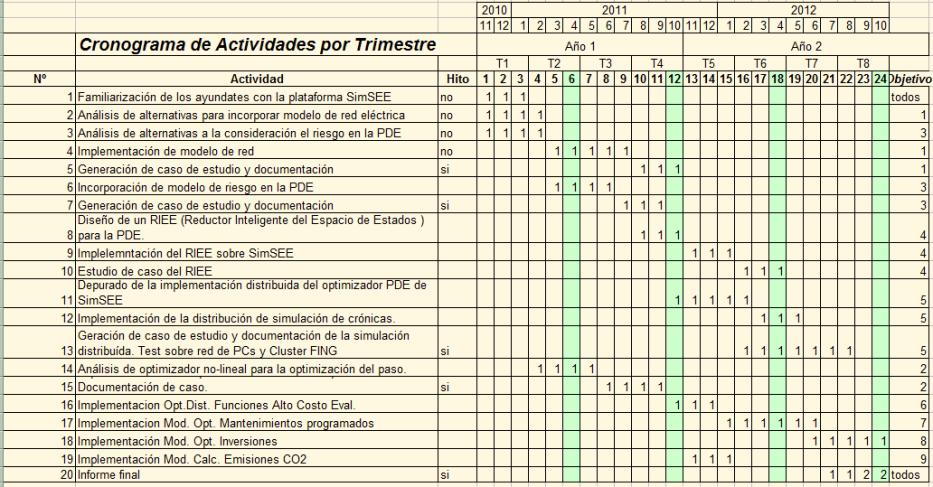
Mejoras a la plataforma de Simulación de Sistemas de Energía Eléctrica - SimSEE

proyecto aprobado: PR_FSE_2009_1_ 18
FONDO SECTORIAL ENERGIA - ANII.
Responsable: Msc. Ing. Ruben Chaer / IIE-FING-UDELAR.

Llamado 1 Asistente (Perfil eléctrico), Llamado 2 Asistentes (Perfil Programadores).

PARTE III.2.- DESCRIPCION

2.1.- Descripción del Proyecto

Sección 1 - Introducción

SimSEE es la plataforma de enseñanza e investigación en Simulación de Sistemas de Energía Eléctrica de la Facultad de Ingeniería (FING) de la Universidad de la República Oriental del Uruguay (UdelaR). Fue desarrollada por el Instituto de Ingeniería Eléctrica (IIE) durante el 2007, en el marco del proyecto de desarrollo tecnológico PDT-47-12 financiado por el BID, bajo la dirección del Dr. Ing. Gonzalo Casaravilla y con el apoyo de Facultad de Ingeniería, MIEM, URSEA, ADME y UTE.

A fines del 2007 FING y la Administración del Mercado de Eléctrico (ADME) celebraron un convenio de cooperación para el mantenimiento y mejora de la plataforma SimSEE que ha permitido mejorar sustancialmente la interfase de usuario e incorporar nuevos modelos específicos de la operación del sistema uruguayo.

El software SimSEE es de uso libre, tanto en su versión compilada como sus códigos fuentes y pueden bajarse del sitio del IIE en Internet.

Desde el punto de vista de tecnología del software, SimSEE está diseñado e implementado totalmente orientado a objetos por lo cual es relativamente sencillo el desarrollo de nuevos modelos y el mantenimiento de los existentes. La incorporación de un nuevo modelo se desarrolla en forma aislada sin necesidad de modificar el resto de los modelos. Esta facilidad para agregar nuevos modelos y/o mejoras de los existentes hace de SimSEE una plataforma ideal para los objetivos de enseñanza e investigación.

Actualmente SimSEE es utilizada en IIE para el dictado del curso de actualización profesional “Simulación de sistemas de Energía Eléctrica - SimSEE” y en ADME y por agentes del mercado para el seguimiento de la operación del sistema, para realizar estudios de planificación y para el análisis de nuevas inversiones.

Entre los alumnos que realizaron el curso del IIE y los usuarios que requirieron el software desde la página de ADME hay 86 usuarios registrados.

Este proyecto plantea agregados/mejoras sobre la plataforma SimSEE con el fin de lograr un mejor modelado de las energías autóctonas.

Sección 2 - Necesidad de introducir mejoras para el correcto modelado de las energías autóctonas.

Para entender el requerimiento de ciertas mejoras en la plataforma SimSEE para el correcto modelado de las energías autóctonas es necesario comprender la complejidad del problema que se resuelve a intentar simular la operación óptima de un sistema de energía eléctrica. En esta sección haremos el intento de explicar en palabras los algoritmos utilizados y los puntos débiles de los mismos.

El planteo de optimización y simulación de sistemas de energía eléctrica en el que intervienen reservorios de energía tiene la complejidad de que la capacidad de almacenar los recursos acopla los pasos de tiempo entre si imposibilitando resolver la optimización de cada paso de tiempo en forma independiente. Un buen planteo del problema es el realizado por Mario Veiga Pereira en [c1-c2].

En la Fig. 1 se muestra un diagrama de bloques del problema de operar en forma óptima el sistema de generación eléctrica. Un bloque corresponde al sistema, con sus vectores de entradas no controladas y controladas . El sistema tiene un vector de estado y un vector de salidas . El otro bloque corresponde al operador del sistema. El operador tiene una Política de Operación (PO) en base a la cual impone al sistema las entradas de control que calcula en base a su PO y la información que puede obtener de , y .

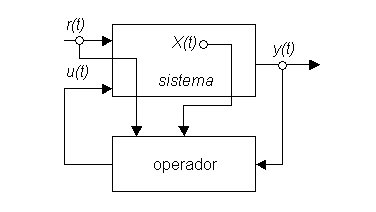
Fig. 1 Diagrama de bloques Sistema y Operador

De todas las PO posibles el operador deberá utilizar aquella que lleve a la operación óptima del sistema cumpliendo con las condiciones de calidad de suministro de la energía establecidas. Normalmente, se dice que una PO es mejor que otra cuando respetando las restricciones propias del sistema conduce a un Costo Futuro (CF) de operación inferior que la otra. Entendemos por CF en un instante dado y para un estado dado del sistema al costo esperado de operar el sistema desde ese instante y condición inicial hasta el fin de los tiempos. El CF es para una PO dada y es el valor esperado en el ensamble de las realizaciones posibles de las entradas no controladas .

Con estas definiciones, el problema de optimizar la PO se reduce a buscar aquella que logra el menor valor de CF para todo tiempo y estado del sistema.

Este es un problema clásico de teoría de control de sistemas y la forma clásica de resolución es mediante el algoritmo conocido como Programación Dinámica Estocástica [c3].

La solución numérica “clásica” usando este algoritmo es recursiva en el tiempo. Se selecciona una ventana de tiempo sobre la que se resuelve el problema y se discretiza esa ventana en pasos de tiempo. La iteración comienza en el último paso de tiempo retrocediendo en el tiempo, paso a paso hasta alcanzar el primer paso de tiempo. En cada paso de tiempo, se debe calcular CF en todo el espacio de estado alcanzable, para ello se discretiza cada una de las componentes de en su posible rango de variación y se calcula CF sobre la malla de puntos correspondiente al producto cartesiano de las discretizaciones en cada componente. Supóngase que es de dimensión 3 y que discretizamos el intervalo en el que puede variar cada componente en N puntos, el producto cartesiano de las discretizaciones define así un hipercubo de NxNxN puntos. Esto lleva a un crecimiento explosivo de la cantidad de los puntos de cálculo en el espacio de estado al aumentar la dimensión . Esta explosión en la cantidad de puntos de cálculo es lo que se conoce como La Maldición de la dimensionalidad de Bellman y es lo que vuelve inoperante el algoritmo al aumentar la cantidad de variables de estado de un sistema.

Una solución más elegante al problema es la conocida como Programación Dinámica Estocástica Dual (PDED o SDDP por sus siglas en inglés) desarrollada en [c4]. Este algoritmo es la aplicación del método de Branch and Bound sobre la iteración recursiva del cálculo de CF. El método es realmente elegante, pero necesita trabajar sobre una función CF convexa, para garantizar la convergencia y que los procesos estocásticos puedan representarse en forma simplificada para que sea realmente efectivo en su lucha contra la maldición de la dimensionalidad. La principal causa de no-convexidad de la función CF la introducen los mínimos técnicos de las máquinas térmicas. Generalmente se simplifica la representación de las centrales térmicas y se las modela como una central, con costo variable igual al costo medio de generación y con un rango de potencia entre 0 y la potencia nominal. Esta simplificación es perfectamente admisible en un sistema grande en el que cada unidad térmica es un proporción minúscula en el total y cuando el objeto del modelado es la planificación de largo plazo, en la que los detalles del despacho no son lo relevante. En sistema uruguayo es pequeño, por lo que las centrales térmicas tienen un porte significativo comparado con el total de la demanda. Adicionalmente, el principal objetivo de las mejoras propuestas, es modelar mejor los efectos sobre el despacho de las energías autóctonas (principalmente la eólica) y es obvia la importancia que tiene para el despacho la necesidad de prender y/o apagar máquinas y mantenerlas por debajo de su potencia nominal para filtrar variaciones del recurso eólico. La misma condición de sistema pequeño hace que los procesos estocásticos deban ser bien representados no pudiéndose hacer simplificaciones como por ejemplo suponer que se multiplican las potencias de las centrales por su factor de disponibilidad. Es posible que en el futuro se implemente este algoritmo también sobre la plataforma SimSEE con el propósito de aumentar su capacidad para enseñanza e investigación, pero por el momento se ha optado por la implementación clásica con miras a una mejor representación de los detalles necesarios para el modelado de las energías autóctonas.

Para la resolución del sub-problema de optimización (en cada punto del espacio de estados y del tiempo durante la iteración) en SimSEE se utiliza un algoritmo de resolución de problemas lineales con programación entera mixta (MIP-Simplex). Esto permite representar adecuadamente problemas lineales, o problemas que se puedan representar como diferentes problemas lineales según el valor de un conjunto de variables enteras. Esto resuelve por ejemplo el modelo de las centrales térmicas con mínimo técnico, pero no resolvería en forma elegante una no linealidad como puede ser la pérdida de salto efectivo en las represas por consecuencia del caudal erogado. Para resolver estas no-linealidades SimSEE tiene implementado un bucle de iteraciones en el que le permite a los distintos sub-modelos variar su representación lineal según los resultados de la optimización. Esta solución funciona, pero es un tanto ineficiente dado que cada iteración implica armar y resolver nuevamente el problema de optimización.

La incorporación de energías autóctonas al sistema (eólica, solar, biomasa) supone la instalación de muchos generadores geográficamente distribuidos. La correcta representación de este nuevo tipo de generación presenta el desafió de realizar la simulación del sistema con un paso de tiempo mucho más fino dado que es necesario representar adecuadamente el poder de filtrado de los lagos del sistema sobre la producción aleatoria de energía de recursos tales como la eólica. Para que sea apreciable el poder de filtrado de los lagos del sistema es necesario representarlos todos como tales con lo cual se deben considerar como variables de estado aumentando la dimensión del estado respecto a lo que se utiliza normalmente. También será necesario representar mejor las restricciones impuestas por la red eléctrica dado que la mayoría de los nuevos emprendimientos se instalarán en ramales poco fuertes de la red pudiendo haber para determinadas configuraciones del sistema o en determinadas horas de pico o valle de las demandas restricciones de tensión a considerar.

Una correcta consideración de la red eléctrica necesariamente lleva a una función de costo no-lineal dado que por ejemplo las pérdidas de una línea varían con el cuadrado de la potencia que transmiten. Esto lleva a pensar en mejorar las rutinas de optimización que actualmente utiliza SimSEE para facilitar la representación de las no-linealidades.

Sección 3 - Objetivos específicos de Investigación e Innovación

En este proyecto de plantean los temas de investigación que se enumeran a continuación y la incorporación inmediata de los resultados a la plataforma SimSEE quedando por lo tanto disponible para el uso público.

Objetivo 1) Desarrollo de un modelo de la red eléctrica aplicable a la simulación del despacho energético de la generación distribuida.

La expansión en base a energías autóctonas es inherentemente distribuida. Esto implica que la forma actual de modelado del sistema como un único nodo en el que se concentra generación y demanda puede no ser la más adecuada para las tareas de planificación y programación de la generación.

Actualmente SimSEE permite la definición de nodos y arcos que posibilitan en forma rústica tener una primer aproximación al problema reflejando en forma rústica los límites de potencia por las líneas de transmisión y las pérdidas en las mismas, pero ignorando por completo posibles problemas de afectación de la tensión de las barras. Al pensarse en una expansión en base a energía eólica y/o centrales de biomasa distribuidas geográficamente e interconectadas al sistema por líneas radiales es claro que será necesario considerar las afectaciones que sobre la tensión tendrán estas instalaciones. Por esta razón se propone incorporar al SimSEE un modelado más fino del sistema de transporte que permita incluir las restricciones sobre las tensiones de los nodos.

Hay abundante literatura sobre cómo realizar esta representación (por ej. [c1] y [c5]). En este proyecto se propone investigar las soluciones existentes e implementar por lo menos una en SimSEE.

Objetivo 2) Optimización no-lineal compatible con la filosofía orientada a objetos actual de SimSEE.

El cálculo de la función de costo futuro en los algoritmos de programación dinámica, se plantea como una fórmula recursiva en la que se resuelve un problema de optimización para cada paso de tiempo. En las herramientas actualmente en uso, la resolución de ese problema de optimización se utiliza un método Simplex. El método es para resolución de sistemas lineales. Esto significa una simplificación que puede no ser adecuada para representar algunos aspectos. En particular vale la pena mencionar la variación del coeficiente energético de las centrales hidráulicas por efecto del caudal erogado (que hace que la potencia generada dependa en forma no lineal con el caudal turbinado) y las pérdidas en las líneas de transmisión (que tienen dependencia cuadrática con la potencia transmitida).

Como una forma de resolver este problema, SimSEE resuelve cada problema de optimización (en cada paso de tiempo en cada punto del espacio de estado y para cada realización de los procesos estocásticos) creando un bucle en el que permite a los diferentes modelos cambiar su representación lineal en base al resultado de la optimización. Este bucle se repite mientras que los modelos estén “desconformes” con el resultado e indiquen que quieren mejorar el modelo con el que se resolvió el problema. Esta iteración es costosa en tiempo de cálculo porque se arma un nuevo problema lineal al inicio de cada iteración que se debe resolver desde cero.

La intención es implementar un optimizador no-lineal compatible con la filosofía de “armado del problema” orienta a objetos de SimSEE.

La implementación orienta a objetos de SimSEE hace que cada modelo sea responsable del “armado del problema” de optimización en cada paso de tiempo. Es así que se hace una “recorrida” por los diferentes Actores (centrales térmicas, hidráulicas, demandas, etc.) para que los mismos agreguen al problema sus variables de control y sus restricciones. Actualmente, como el problema es linealizado, el armado del problema se realiza cargando coeficientes en una matriz del problema.

La idea es investigar la posibilidad de mantener esta representación, pero que en lugar de simples coeficientes, los modelos puedan cargar funciones un poco más complejas, lo que implicará que no se pueda utilizar el Simplex para la resolución del problema.

De esta forma no sería necesario realizar iteraciones para mejorar la representación.

Objetivo 3) Una alternativa a la función de costo de operación futuro, como función objetivo, que permita considerar la aversión al riesgo.

Actualmente la optimización de los recursos energéticos con fines de la programación del despacho se realiza resolviendo un problema de optimización dinámico estocástico cuya función objetivo a minimizar es el valor esperado del costo de operación futuro del sistema. Como resultado de la optimización de obtiene la valorización del agua de los embalses del sistema para cada estado posible.

Del uso profesional de SimSEE realizado en ADME para el seguimiento de la operación del sistema se ha observado que el costo de operación anual del sistema es poco sensible a errores en la valorización del agua de los embalses. Esto lleva en forma inmediata a la observación de que es posible afectar la valorización del agua (y por consiguiente adelantar o atrasar su uso) sin grandes cambios en el costo esperado de operación del sistema. Esto significa que la función objetivo (valor esperado de la operación futura del sistema) es bastante “chata” alrededor de la solución óptima.

Esto nos permite pensar en otro criterio adicional a la minimización del valor esperado del costo futuro para la selección de la política de operación dentro del conjunto de las soluciones que se pueden considerar similares.

Un criterio adicional posible puede ser disminuir el riesgo de costos elevados. Es decir, dentro del conjunto de las aceptables elegir aquella solución que además minimiza el riesgo de incurrir en costos elevados.

Dado que el agregado de las energías autóctonas, principalmente de la eólica presupone aumentar la aleatoriedad de los recursos del sistema es de esperar que el conjunto de soluciones aceptables sea aún más grande si solo se mira el costo en valor esperado.

A modo de ejemplo de cómo considerar el riesgo desde el punto de vista del sistema y desde el punto de vista de un agente se puede ver la referencia [c6] que muestra la aplicación de un criterio de aversión al riesgo en la operación del mercado brasilero y la referencia [c7] muestra la consideración del riesgo en la planificación de inversiones en generación.

Se propone en este trabajo investigar una representación del riesgo dentro del algoritmo de optimización dinámica estocástica e implementarlo en la plataforma SimSEE.

Objetivo 4) Reducción inteligente del espacio de estados en el algoritmo de programación dinámica estocástica.

Como se mencionó en la sección 2 la PDE implica la discretización del espacios de estado del sistema lo que lleva la Maldición de la Dimensionalidad de Bellman y hace que la programación dinámica estocástica deje de ser aplicable si crece la cantidad de variables que es necesario considerar.

Esto lleva a simplificaciones del modelo del sistema para evitar incluir variables de estado. A modo de ejemplo, en simulaciones de horizontes largos de tiempo (aplicables a estudios de planificación) se considera como variable de estado solamente el volumen embalsado de la represa de Rincón de Bonete más una variable de estado adicional que intenta representar la situación del sistema hidrológico. En simulaciones de más corto plazo, como puede ser la programación del despacho semanal es posible (y necesario) incluir en el modelado más variables de estado como pueden ser el volumen en las represas de Palmar y Salto Grande.

Para modelar correctamente los tiempos de arranque y parada de las centrales térmicas sería necesario incluir más variables de estado pero actualmente no es práctico hacerlo salvo para simulaciones de muy corto plazo.

Observando los resultados de la Programación Dinámica Estocástica se observa que la función de costo futuro se podría representar con menos variables que las consideradas, buscando una descripción paramétrica de la misma. La idea es identificar el tipo de función que mejor aproxima a la función de costo futuro y calcular solamente los puntos del espacio de estado necesarios para ajustar los parámetros de la función.

Este proceso implicaría la resolución completa en algunos pasos de tiempo para seleccionar nuevamente del conjunto de funciones la que mejor aproxima y en cada paso de tiempo una resolución parcial (solo en los puntos necesarios) para la calibración de los parámetros.

Otra idea para atacar el problema de la dimensionalidad de Bellman es crear un algoritmo similar a lo descrito en el punto anterior, pero el tipo de parametrización y su calibración sea mejorado por medio de programación genética. Dado que la optimización se ejecuta muchas veces sobre el mismo sistema es de esperar que el resultado de este tipo de optimización pueda ir mejorando casi en forma continua. Por ejemplo, la optimización se ejecuta todas las semanas para realizar la programación semanal del despacho y luego todos los días se ejecuta nuevamente para ir haciendo la programación diaria. Otra ventaja de este enfoque es que es fácilmente distribuible en una red de cálculo, dado que cada individuo de una generación puede calcular su índice de desempeño independientemente del resto.

En este proyecto se plantea investigar e implementar la representación paramétrica de la función de Costo Futuro e investigar la factibilidad de realizar la calibración mediante programación genética dejando todo preparado para otro proyecto de investigación en este sentido si se considerara que esta vía es factible.

Objetivo 5) SimSEE distribuido.

Otra forma de luchar contra el tiempo de cálculo es la posibilidad de distribuir el cálculo entre varias computadoras o nodos de cálculo.

En SimSEE ya se dispone de una implementación en que la PDE se realiza en forma distribuída entre un conjunto de nodos de cálculo que pueden ser simples PCs conectados a una red de datos o equipos de computación del alta performance como el CLUSTER adquirido recientemente en FING. Con esta implementación experimental se realizaron algunas pruebas que muestran las posibilidades de esta solución [c8]. La implementación actual es de uso interno del equipo de investigación y ha servido para testear la factibilidad de lo que se propone.

En este proyecto se propone mejorar la implementación disponible para que sea utilizable por el público en general integrándola a la aplicación que instalan los usuarios en sus PCs.

La idea es permitir a cada PC con una instalación de SimSEE que sirva como nodo de la red de cálculo. El usuario en todo momento podrá habilitar o no el funcionamiento en red y el rango de las IPs con las que forma red. De esta forma la plataforma es instalable en un grupo de PCs en cualquier institución. Si bien podría usarse para interconectar PCs vía Internet los tests realizados indican que para que tenga sentido la distribución del algoritmo de PDE es necesaria una velocidad de comunicación importante entre los nodos de cálculo.

Como se explicó en la sección 2 en SimSEE hay usa un algoritmo de PDE para la obtención de la PO óptima. La PDE se resuelve en forma iterativa necesitándose la solución de un paso de tiempo para resolver la del paso siguiente. En cada paso de tiempo se deben resolver un problema de optimización para cada punto del espacio de estado.

En la implementación realizada en SimSEE del PDE distribuido, se parte el espacio de estado en zonas y se distribuye el trabajo de cálculo entre los nodos. La necesidad de conocer lo que calcularon los demás nodos en cada paso de tiempo implica la necesidad de un gran flujo de comunicación entre los nodos en cada paso de tiempo para comunicarse entre si los resultados de cada uno.

Luego, de la optimización para obtener la PO óptima, se realizan generalmente una o más simulaciones en las que se considerar muchas realizaciones de los procesos estocásticos (o crónicas). Los resultados se obtienen entonces por la simulación de muchas crónicas diferentes operando el sistema con la PO. Estas simulaciones se pueden realizar en forma totalmente independiente por lo que son fácilmente paralelizables.

Se realizará una implementación de la PDE en forma distribuida (mejorando la disponible actualmente) y se implementará la distribución de la etapa de Simulación.

Para la presentación de los resultados se mostrará el tiempo de cálculo completo de realizar una programación semanal del sistema uruguayo tal como se realiza en ADME para el seguimiento de la operación del sistema. Se presentarán los resultados de las corridas en un sólo PC, en la red del laboratorio de software del IIE (18 PCs) y el CLUSTER de FING (equipo de 72 nodos de cálculo formado por 9 tarjetas de 8 núcleos cada una).

La implementación distribuida de la plataforma SimSEE implicará que se pueda agregar detalle al modelado del sistema lo que es fundamental para los objetivos de investigación de la misma. Poder analizar los resultados de un mejor modelo nos permite realizar simplificaciones para la operación cotidiana del sistema que de otra forma son realizadas con aproximaciones rústicas.

Objetivo 6) Creación de Optimizador Distribuido para Funciones de Alto Costo de Evaluación.

La idea es aprovechar la capacidad de distribuir tareas para implementar un Optimizador Distribuido aplicable a problemas con función objetivo de alto costo de evaluación.

Por función objetivo de alto costo de evaluación nos referimos a funciones en que evaluar el valor de la función en un punto insume un tiempo de cálculo considerable. En el contexto que nos interesa típicamente la función objetivo es el resultado de correr la optimización y simulación de un sistema para evaluar por ejemplo el costo esperado de abastecimiento de la demanda. Es decir, la función objetivo incluye la ejecución de la optimización y de la simulación en un conjunto de crónicas apreciables como para poder calcular el valor esperado con soporte estadístico suficiente.

Hay determinadas tareas como por ejemplo la optimización de los mantenimientos de las centrales de generación o la selección de un plan de inversiones en generación que llevan a problemas de optimización con variables enteras en los que no hay más remedio que probar muchas combinaciones de soluciones. Nuestra idea es implementar un optimizador, que simplemente aplique el método de fuerza bruta para recorrer las combinaciones distribuyendo en la red de nodos de calculo la ejecución del programa que evalúa la función de costo. Se implementará un mecanismo de comunicación entre los nodos que realizan la optimización distribuida de forma de que en todo momento todos puedan saber la mejor solución factible encontrada. Esto permitirá suspender una evaluación en proceso si el evaluador puede inferir en forma temprana que no logrará un costo inferior al de la mejora solución encontrada.

Se implementará un módulo que permita especificar un programa ejecutable como función de evaluación y un formato de definición de parámetros modificables para actuar sobre ellos.

Se implementará un módulo que permita utilizar el optimizador para la planificación de los mantenimientos programados de las centrales y otro para la optimización de las inversiones en generación.

Objetivo 7) Módulo de optimización de los mantenimientos programados de las centrales de generación.

Las centrales de generación necesitan determinadas rutinas de mantenimiento para garantizar su correcto funcionamiento. Dependiendo del tipo de central los días de parada necesarios son diferentes. Típicamente, a modo de ejemplo, las necesidades de mantenimiento son entre 15 y 30 días por año y una vez cada cuatro años un mantenimiento mayor de 2 o 3 meses.

El administrador del sistema debe programar los mantenimientos de forma de afectar lo menos posible el sistema. Se creará una aplicación que permita especificar las necesidades de mantenimiento de las centrales de generación sobre una Sala de SimSEE y definir así un problema de optimización para ser resuelto con el optimizador desarrollado en el Objetivo 6.

Objetivo 8) Algoritmo de optimización de las inversiones que determinan la expansión del parque generador.

El crecimiento de la demanda eléctrica necesita ser acompasado con instalación de nueva potencia en el sistema. Puede diseñarse la potencia a instalar con diferentes criterios en cuanto a la cantidad y tipo de potencia. El reglamento de mercado mayorista [9], indica cómo calcular el faltante de potencia firme en el sistema. Este es un indicador de la potencia faltante, pero es potencia puede ser cubierta por diferentes proyectos de inversión con diferentes costos de inversión, plazos para construcción y costos variables de producción y de operación y mantenimiento. El objetivo de la optimización del plan, es encontrar aquel plan que cumpliendo con el criterio de respaldo necesario sea el económicamente mejor. También es posible plantear el problema de respaldo dentro de la función de costos pudiéndose entonces definir una función objetivo a minimizar.

Las variables de la optimización son las diferentes alternativas de inversión de una cartera de proyectos posibles en determinadas ventanas de tiempo.

Se desarrollará una aplicación que permita definir la cartera de posibles proyectos de generación sobre una Sala de SimSEE y genere la descripción del problema de optimización para ser resuelto con el optimizador desarrollado en el Objetivo 6..

Objetivo 9) Módulo de cálculo del factor de emisiones del sistema eléctrico

Una componente importante en los nuevos proyectos de inversión en generación renovable es la venta de certificados de reducción de emisiones (CERs) bajo el Mecanismo de Desarrollo Limpio (MDL) del Protocolo de Kioto.

Dentro de las etapas que deben seguirse para la obtención de los mismos se encuentra la confección del PDD (Project Design Document), el cual requiere la estimación de la reducción de emisiones del proyecto.

La metodología para este cálculo es la especificada en el documento, “Tool to calculate the emisión factor for an electric system” (UNFCCC, http://cdm.unfccc.int/methodologies/PAmethodologies/tools/am-tool-01-v5.2.pdf ).

La misma está basada en el cálculo del Margen de Operación (Operating Margin, OM) y del Márgen de Construcción (Build Margin, BM), que se utilizan para determinar el Margen Combinado (Combined Margin, CM).

La forma más apropiada para estimar la reducción de emisiones del proyecto es realizando una simulación de la operación futura del sistema durante la vida util del mismo y utilizar los resultados para calcular el CM.

Se desarrollará dentro del SimSEE un módulo de cálculo para el factor de emisiones esperado del sistema eléctrico, basado en la Metodología mencionada de la UNFCCC.

Referencias.

[ c1] B.G.GORENSTIN N.M.CAMPODONICO J.P.COSTA M.V.F.PEREIRA. STOCHASTIC OPTIMIZATION OF A HYDRO-THERMAL SYSTEM INCLUDING NETWORK CONSTRAINTS. Transactions on Power Systems, Vol. 7, No. 2. May 1992.

[ c2] M.V.F. Pereira and L.M.V.G. Pinto. A DECOMPOSITION APPROACH TO THE ECONOMIC DISPATCH OF HYDROTHERMAL SYSTEM. IEEE Transactions on Power Apparatus and Systems, Vol. PAS-101, No. 10 October 1982 3851.

[ c3] Bellman, R. Dynamic Programming, Princeton University Press, 1957.

[ c4] M.V.F. Pereira, L.M.V.G. Pinto, Multi stage stochastic optimization applied to energy planning, Mathematical Programming, 359-375 52, 1991.

[c5] Olav Bjarte Fosso, Seyed Mohammed, Ali Hosseini.Hydro scheduling with transmission transfer limitations in a liberalized power market. XI SEPOPE, 16 a 20 de Março 2009March – 16th to 20th – 2009BELÉM (PA) - BRASIL.
http://webserver.eln.gov.br/sepope/dad/temas_rel.asp

[c6] ONS NT 007/2004, METODOLOGIA DE INCORPORAÇÃO DA CURVA DE AVERSÃO A RISCO AO MODELO NEWAVE MÉTODO CAR.
http://www.aneel.gov.br/aplicacoes/audiencia/arquivo/2004/001/documento/nt_007_2004_metodologia_car.pdf

[c7] Leonardo Soares, Alexandre Street, Priscila Lino, Sérgio Granville, Luiz A. Barroso, André Resende Guimarães, Mario Veiga Pereira. PRECIFICAÇÃO E SELEÇÃO DE NOVOS EMPREENDIMENTOS DE GERAÇÃO NO SETOR ELÉTRICO BRASILEIRO: UM ENFOQUE RISCO RETORNO. SNPTEE, 14 a 17 Outubro de 2007, Rio de Janeiro-Brasil.
http://www.psr-inc.com/psr/download/papers/SNPTEE_Artigo_R-Retorno_V2.pdf

[c8] Pablo Alfaro, Ruben Chaer, NetTopos: una plataforma de cálculo distribuido diseñada para el Simulador de Sistemas de Energía Eléctrica SimSEE. Encuentro de Potencia, Instrumentación y Medidas, EPIM 08. Montevideo, Uruguay., page 45--51 - 16-17 oct. 2008.
http://iie.fing.edu.uy/publicaciones/2008/AC08/AC08.pdf

[c9] Ministerio de Industria, Energía y Minería.Decreto Nº 360/002 – Reglamento del Mercado Mayorista de Energía Eléctrica.